Line equation
STEP 1: graph of the given points
We have two given values:
In 2011 the car costs $45,000
In 2015, the car costs $37,000.
Let's graph this function, the x-axis is going to be the years and the y- axis the cost.
Then, we are going to locate y=45000 at x=2011:
(2011, 45000)
and y=37000 at x=2015:
(2015, 37000).
STEP 2: line graph
We want to find a function for the straight line that connects the points:
STEP 3: line equation
We know that the equation of a line is given by:
y =mx + b
where m and b are numbers: m is the slope (it shows the inclination of the line) and b is the y-intercept.
We want to find m and b to obtain the equation.
m: slope
We have two points (first step):
(x₁, y₁) = (2011, 45000)
(x₂, y₂) = (2015, 37000)
We find the change of each variable from point 1 to point 2:
Δx = x₂ - x₁ = 2015 - 2011
= 4
Δy = y₂ - y₁ = 37000 - 45000
= -8000
We have that the slope is given by the rate between Δy and Δx:
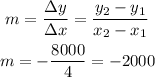
Then m = -2000, so this line equation should look like:
y =mx + b
↓
y = -2000x + b
b: y-intercept
In order to find b we replace x and y in the equation by a value we know they should have.
We have that when it is x=2011, then y=45000. Let's replace:
y = -2000x + b
↓
45000= -2000 · 2011 + b
Let's solve the equation for b:
45000= -2000 · 2011 + b
↓since -2000 · 2011 = -4,022,000
45,000= -4,022,000 + b
↓ taking -4,022,000 to the left
45,000 +4,022,000 =b
4,067,000=b
Then b= 4,067,000, so this line equation should look like:
y = -2000x + b
↓
y = -2000x + 4,067,000
Answer A: a linear model is y = -2000x + 4,067,000
STEP 4: estimate to the current value of Joe's car
This is the year 2021. This means that x=2021. Let's replace in the equation and see what happens with y (the price of the car) this year:
y = -2,000x +4,067,000
↓
y = -2,000 ·2021 +4,067,000
Since -2,000 ·2021 = -4,042,000
y = -4,042,000 +4,067,000
y = 25,000
This means that the current value of the car is $25,000
Answer B: the current value of Joe's car is $25,000
STEP 5: estimate to the value of Joe's car in 2012
In 2012, x=2012. Replacing in the equation:
y = -2,000x +4,067,000
↓
y = -2,000 ·2012 +4,067,000
Since -2,000 ·2012 = -4,024,000
y = -4,024,000 +4,067,000
y = 43,000
Answer C: in 2012 the value of Joe's car was $43,000