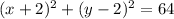Question

Which equation represents a circle with a center located at ( -2, 2) and a circumference of 16 pi?

Answer 1

Step-by-step explanation:

The equation of a circle with center located at (x1, y1) and radius r is:

`(x-x_1)^2+(y-y_1)^2=r^2`

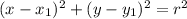
We have the point but we need to find r. For that we can use the equation of the circumference:

`C=2\pi r`

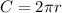
We have C = 16pi:

`\begin{gathered} 16\pi=2\pi r \\ (16\pi)/(2\pi)=r \\ r=8 \end{gathered}`

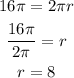
Now we have r = 8, therefore r²=64. The answers could be either option 1 or option 3. To find out which one is it we have to check the point.

If the point is (-2, -2) then the part with x is (x - (-2))² = (x+2)² and the part with y is (y - 2)²

Answer:

The correct equation is option 3:

`(x+2)^2+(y-2)^2=64`