Question

Use two equations in two variables to solve the application.Peter invested some money at 6% annual interest, and Martha invested some at 12%. If their combined investment was $4,000 and their combined interest was $360, how much money (in dollars) did Martha invest?

Answer 1

Given

Peter invested some money at 6% annual interest, and Martha invested some at 12%. If their combined investment was $4,000 and their combined interest was $360, how much money (in dollars) did Martha invest?

Solution

Let Peter's investment be X

Let Martha's investment be Y

`\begin{gathered} x+y=4000\ldots Equation\text{ (i)} \\ 0.06x+0.12y=360\ldots Equation\text{ (i}i) \end{gathered}`

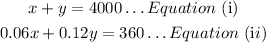
I will solve your system by substitution.

(You can also solve this system by elimination.)

Step 1

`\begin{gathered} x+y=4000 \\ \text{make x the subject of the formula},\text{ therefore we substract y from both sides} \\ x+y-y=\text{ 4000-y} \\ x=4000-y \end{gathered}`

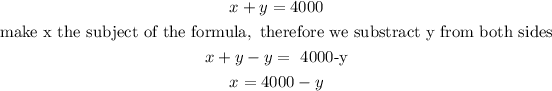
Step 2

Substitute for x in Equation (ii)

`\begin{gathered} 0.06(4000-y)+0.12y=360 \\ 240-0.06y+0.12y=360 \\ 240+0.06y=360 \\ \text{make y the subject of the formula} \\ 0.06y=360-240 \\ 0.06y=120 \\ \text{Divide both sides by 0.06} \\ (0.06y)/(0.06)=(120)/(0.06) \\ \\ y=2000 \end{gathered}`

Step 3

`\begin{gathered} \text{Substitute for y in equation (i)} \\ x+2000=4000 \\ x=4000-2000 \\ x=2000 \end{gathered}`

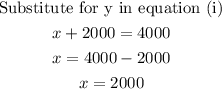
The final answer

Martha's investment is $2000