Solution:
The determine the end behavior of the function below
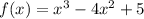
We will use the image of the function below
The end behavior of a function f describes the behavior of the graph of the function at the "ends" of the x-axis. In other words, the end behavior of a function describes the trend of the graph if we look to the right end of the x-axis (as x approaches +∞ ) and to the left end of the x-axis (as x approaches −∞ ).
Step 1:
From looking at the graph above, we can see that
Since the leading term of the polynomial (the term in the polynomial which contains the highest power of the variable) is x3, the degree is 3, i.e. odd, and the leading coefficient is 1, i.e. positive.
The domain of the function is given below as
![-\infty<strong>Therefore,</strong><p><strong>The end behavior of the function above is</strong> </p>[tex]\begin{gathered} x\rightarrow+\infty,f(x)\rightarrow+\infty,\text{and} \\ x\rightarrow-\infty,f(x)\rightarrow-\infty \end{gathered}]()