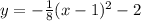Answer:
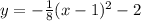
First, to know the opening of the parabola, let us solve for p:
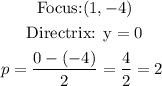
Now, the formula for the parabola is noted as:
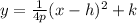
Since our p is 2, the vertex of the parabola would be at:

This will now be our (h,k).
With these, we know that
h = 1
k = -2
p = 2
We substitute these values to the equation:
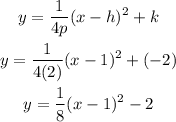
Since our parabola is opening downward, we will add a negative sign in front of the equation.
The equation is, therefore: