Question

Translate to system Juan is studying for his final exams in Chemistry and Algebra. He knowshe only has 24 hours to study, and it will take him at least three times aslong to study for Algebra than Chemistry.

Answer 1

Let A be the amount of hours that Juan can study for Algebra and C the amount of hours that he can study for Chemistry.

Since the total amount of time that he can study is 24 hours, then:

`A+C=24`

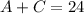
Since he will study Algebra three times as long as he will study Chemistry, then:

`A=3C`

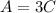
Then, a system of equations that represents this set of conditions for the study time, is:

`\begin{gathered} A+C=24 \\ A=3C \end{gathered}`

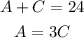
This system can be solved using the substitution method. Replace A=3C into the first equation and solve for C:

`\begin{gathered} A+C=24 \\ \Rightarrow3C+C=24 \\ \Rightarrow4C=24 \\ \Rightarrow C=(24)/(4) \\ \\ \therefore C=6 \end{gathered}`

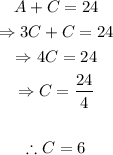
Replace C=6 into the expression for A:

`\begin{gathered} A=3C \\ \Rightarrow A=3(6) \\ \\ \therefore A=18 \end{gathered}`

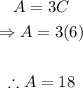
Therefore, the system of equations that represents the given situation is:

`\begin{gathered} A+C=24 \\ A=3C \end{gathered}`

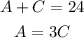
And the solution says that Juan has 18 hours to study for Algebra and 6 hours to study for Chemistry.