Given:
a.) A new tire had a tread depth of 5 over 8 in. (5/8)
b.) After driving one year the tire had 17 over 32 in. of tread remaining. (17/32)
First, let's make the two fractions 5/8 and 17/32 into similar terms. (With the same denominator)
The LCM of 8 and 32 is 32. Therefore, let's transform 5/8 into its equivalent fraction with a denominator of 32.
We get,
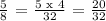
Therefore, the original tire depth is 5/8 or 20/32 in.
Next, let's determine the difference between the original and new depth after one year.

3/32 in. of the thread was worn out. Let's now determine its equivalent percentage.
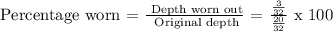
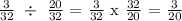

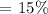
Therefore,
The answer is 15%.15% of the thread was worn after a year.
The answer is 15%.