Answer:
![x=1+\frac{\sqrt[]{40}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/dl7og591c8npp835c1o3o95oagbgatpii4.png)
Step-by-step explanation: Given the folllowing equation, we need its positive solution or root:
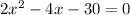
Solution by Quadratic formula:
![x=\frac{-B\pm\sqrt[]{B^6-4AC}}{2S}\rightarrow(1)](https://img.qammunity.org/2023/formulas/mathematics/college/owwiikt89cj9529cipehjnw9j24by8vla5.png)
Where x can be positive and negative, but we are interested in the positive solution.
Constants A B C in (1) are as follows:
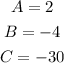
Plugging these values in (1) gives us:
![x=\frac{-(-4)\pm\sqrt[]{(-4)^2-4(2)(-30)}}{2(2)}=\frac{4\pm\sqrt[]{16+(8)(30}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/6gxujajy5ftjjpni31gx3fgrk6ynqauhe9.png)
Firther simplification gives:
![\begin{gathered} x=\frac{4\pm\sqrt[]{16+24}}{4}=\frac{4\pm\sqrt[]{40}}{4}\rightarrow positive\rightarrow x=\frac{4+\sqrt[]{40}}{4}=1+\frac{\sqrt[]{40}}{4} \\ \therefore\rightarrow \\ x=1+\frac{\sqrt[]{40}}{4} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/anrxx8ztpviej1vsv5nfkys9tvgc1qyrqb.png)