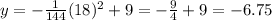Answer:
Equation of the parabola:
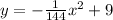
The height of the arch 18 meters from the center is 6.75m
Step-by-step explanation:
The arch feet are 72m apart and the origin half way between them. This means that the axis of symmetry (or the x.coordinate of the vertex) is x = 0
Since it's an arch, the parabola is concave down, with it's maximum at the vertex, y = 9. This means that the vertex is at (0, 9). Also, we can see that the y-intercept is y = 9
Finally, we know the two roots of the parabola: x = -36 and x = 36. This is because the points x = -36 and x = 36 are 72m apart, with the center at the original, as the problem says. SInce x = 36 is a root, this means that at that point the y value is 0.
With all this, we can try to find the general form of a parabola. The general form is:
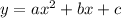
c is the y-intercept. We know that c = 9
We can find the value of b, because we know the coordinates of the vertex. The x-coordinate of the vertex is:
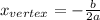
SInce the x-coordinate of the vertex is x = 0
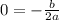
If we solve:
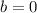
So far we have:
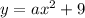
Finally, to find a, we can use the point (36, 0) (one of the roots)
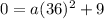
And solve:
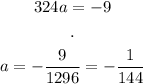
Thus, the equation of the arch is:
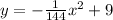
Evaluating this equation for x = 18, we can find the height of the arch: