Given:
AG = 8 inches
BF is the mid-segment of triangle ADG.
CE is the mid-segment of triangle DBF.
Solution.
A midsegment of a triangle is a segment that connects the midpoints of two sides of a triangle.
From the mid-segment theorem, the segment joining the midpoints of two sides of a triangle is parallel to and half the length of the third side.
Hence,

Similarly, CE is a mid-segment of the triangle DBF, hence:
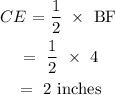
Answer: 2 inches (option A)