Question

AIJK = APQR. If mzi = 3x + 4and mZP = 72 – x, thendetermine the value of x.

Answer 1

Given:

• ΔIJK ≅ ΔPQR

,

• m∠I = 3x + 4

,

• m∠P = 72 - x

Let's find the value of x.

Since both triangles are congruent, their corresonding angles will be equal.

The corresonding angles are:

∠I = ∠P

∠J = ∠Q

∠K = ∠R

To find the value of x given that both triangles are congruent, we have:

`\begin{gathered} m\angle I=m\angle P \\ \\ 3x+4=72-x \end{gathered}`

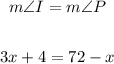
Let's solve for x.

Subtract 4 and add x to both sides:

`\begin{gathered} 3x+x+4-4=72-4-x+x \\ \\ 4x=68 \end{gathered}`

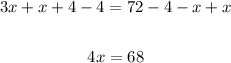
Divide both sides by 4:

`\begin{gathered} (4x)/(4)=(68)/(4) \\ \\ x=17 \end{gathered}`

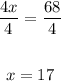
Therefore, the value of x is 17

ANSWER:

17