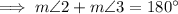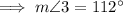Answer:
A. x = 18
B. m∠2 = 68°
C. m∠2 = 112°
Explanation:
Given:
Part A
Vertical Angles Theorem
When two straight lines intersect, the opposite vertical angles are congruent.
Therefore:

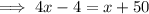
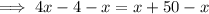

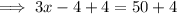
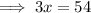
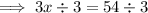
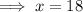
Part B
To find the measure of ∠2, substitute the found value of x into the given expression for ∠2:
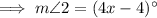
![\implies m\angle 2 =[4(18)-4]^(\circ)](https://img.qammunity.org/2023/formulas/mathematics/high-school/wgn72cz01t6wkrqyynbbese1ms2ahjakzf.png)
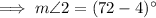
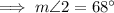
Part C
Angles on a straight line sum to 180°: