GIVEN:
We are told that Jane wanted to buy a set of furniture for $1400. The terms are, 2-year loan at the rate of 18% per annum.
Required;
To determine how miuch her annual payment will be. Also, how much interest will she be paying?
Step-by-step solution;
We begin b y identifying the following;
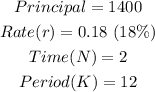
The monthly payment will now be determined by the formula below;
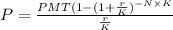
Now we substitute values;

Therefore, the monthly payment will be $69.89 (approximately).
Therefore, annual payments will be;
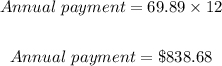
To determine her interest payment we calculate her total payments as follows;
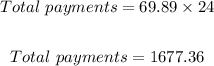
The interest payment therefore would be;

Therefore;
ANSWER:
(a) Annual payment = $838.68
(b) Interest paid = $277.36