According to the problem, angles E and F are equal. Angles D and G are equal.
Also, if the trapezoid is isosceles, then FG = DE by definition. So, we express the following
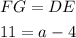
Let's solve for a
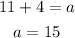
We already know that the sum of all the interior angles is 360°.
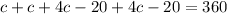
Let's solve for c
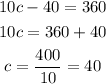
Then, we find each angle using the value of c
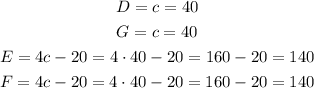
Hence, angles D and G measure 40°, angles E and F measure 140°.