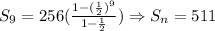Question

find the indicated sum for each geometric series.Pleaseee someone help I need this before 10 pm. I tried to do it but I keep failing.

Answer 1

We will have that it is solved as follows:

`\sum ^9_(k=1)256((1)/(2))^(k-1)=256+128+64+32+16+8+4+2+1=511`

***

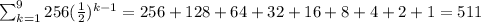
To solve we replace the values in the formula given:

`S_n=a_1((1-r^n)/(1-r))`

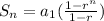
Now, we have to determine the ratio, which is 1/2, and since we want to know the value at n = 9 and the fist value of the series (a1) is 256, we replace it as well:

`S_9=256((1-((1)/(2))^9)/(1-(1)/(2)))\Rightarrow S_n=511`