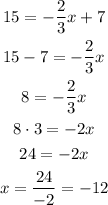Question

I need help with a question

Answer 1

We have the function:

`y=-(2)/(3)x+7`

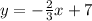
When we have the value of x, and we want to find the value of y, we replace x in the equation and calculate.

For x=-6, we have:

`y=-(2)/(3)\cdot(-6)+7=(-2\cdot6)/(3)+7=-(12)/(3)+7=-4+7=3`

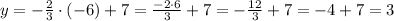
The value of y for x=-6 is y=3.

When we know y, and we want to know the value of x, we replace y and calculate.

For y=5, we have:

`\begin{gathered} 5=-(2)/(3)x+7 \\ 5-7=-(2)/(3)x \\ -2=-(2)/(3)x \\ x=-2\cdot(-(3)/(2))=(2\cdot3)/(2)=3 \end{gathered}`

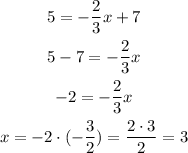
For y=5, the value of x is x=3.

We repeat this for the last two cases:

x=15, the value of y is y=17

`y=-(2)/(3)(15)+7=10+7=17`

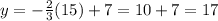
y=15, the value of x is x=-12

`\begin{gathered} 15=-(2)/(3)x+7 \\ 15-7=-(2)/(3)x \\ 8=-(2)/(3)x \\ 8\cdot3=-2x \\ 24=-2x \\ x=(24)/(-2)=-12 \end{gathered}`