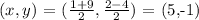Answer:
B ; (4,3) and (5,-1)
Step-by-step explanation:
Here, we want to get the coordinates of the endpoints of the midsegments
Let us firstly give a representation of what we are to calculate:
Now, from the above, what we are to calculate are the coordiantes of the points A and B
If we notice, the point A is the midpoint of the line XY
the point B is the midpoint of YZ
By simply finding the midpoint coordiantes of these lines, we will able to get what we are looking for
We start as follows:
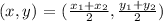
The above will give us the coordiantes of the midpoints
Let us get the coordinates of the individual vertex points
X is (7,4)
Y is (1,2)
Z is (9,-4)
So, for point A that lies between X and Y, we have its coordiante as:
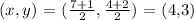
Lastly for point B that lies between Y and Z , we have: