Question

Suppose θ is an angle in the standard position whose terminal side is in Quadrant I and . Find the exact values of the five remaining trigonometric functions of θ.

Answer 1

To answer this question, we can graph the situation as follows:

We graphed a right triangle to express one of the given trigonometric ratios: sin(Θ). We need to find x using the Pythagorean Theorem to find the values of the other five trigonometric functions. Then we have:

`x^2+84^2=85^2\Rightarrow x^2=85^2-84^2\Rightarrow\sqrt[]{x^2}^{}=\sqrt[]{85^2-84^2}`

Then, we have:

`x=\sqrt[]{169}\Rightarrow x=13`

Now we can express the exact values of the five remaining trigonometric functions:

The exact value for cosine function:

`\cos (\theta)=\frac{\text{adj}}{\text{hyp}}\Rightarrow\cos (\theta)=(13)/(85)`
`\tan (\theta)=\frac{opposite}{\text{adjacent}}=(84)/(13)\Rightarrow\tan (\theta)=(84)/(13)`

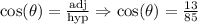
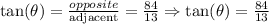
The exact value for the tangent function is shown above.

Now the other exact values for the other trigonometric functions are:

Cosecant: