To answer this question, we can graph the situation as follows:
We graphed a right triangle to express one of the given trigonometric ratios: sin(Θ). We need to find x using the Pythagorean Theorem to find the values of the other five trigonometric functions. Then we have:
![x^2+84^2=85^2\Rightarrow x^2=85^2-84^2\Rightarrow\sqrt[]{x^2}^{}=\sqrt[]{85^2-84^2}](https://img.qammunity.org/2023/formulas/mathematics/college/yrtdx3n6dovsaq49robihnmwfuyoqvxwq4.png)
Then, we have:
![x=\sqrt[]{169}\Rightarrow x=13](https://img.qammunity.org/2023/formulas/mathematics/college/kj4jcuok72sppvh7s3g3awt8905y0g4yjg.png)
Now we can express the exact values of the five remaining trigonometric functions:
The exact value for cosine function:
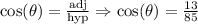
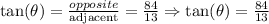
The exact value for the tangent function is shown above.
Now the other exact values for the other trigonometric functions are:
Cosecant:
![undefined]()