Question

Andy needs to create an open topped box to carry a catapult to school for physics class. He uses a piece of cardboard that is 40 inches by 50 inches to make the box, and plans to cut out square corners of measure x inches. What is the maximum possible volume of the box?

Answer 1

Hello there. To solve this question, we'll have to remember some properties about maximizing volumes of boxes.

Let's start by drawing the situation:

In the left, we have the cardboard piece that was 40 inches by 50 inches, then on the right we have it after cutting the square corners of measure x inches.

Now, we create a box by closing the walls:

The measures of the cardboard piece after having been cut the corners are 40 - 2x and 50 - 2x, while after in the box format, its height is equal to x.

Therefore, the total volume of the box is given by:

`x\cdot(50-2x)\cdot(40-2x)=4x^3-180x^2+2000x`

To maximize this function, we take its derivative and find the roots of the polynomial:

`(4x^3-180x^2+2000x)^(\prime)=12x^2-360x+2000`

Taking its roots, we get:

`\begin{gathered} 12x^2-360x+2000=0 \\ \\ x=\frac{360\pm\sqrt[]{360^2-4\cdot12\cdot2000}}{2\cdot12}=\frac{360\pm40\sqrt[]{21}_{}}{24}=15\pm5\sqrt[]{(7)/(3)} \end{gathered}`

In this case, we got two values, but only one of them will maximize this function.

Taking the second derivative of the function, we get:

`(4x^3-180x^2+2000x)^(\prime\prime)=24x-360`

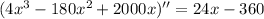
Plugging the values in, we get:

`\begin{gathered} 24\cdot\frac{360+40\sqrt[]{21}}{24}-360=40\sqrt[]{21} \\ \\ 24\cdot\frac{360-40\sqrt[]{21}}{24}-360=-40\sqrt[]{21} \end{gathered}`

And the value such that f''(x) < 0 will be the value that gives us the maximum volume of the box.

Plugging it into the expression for the volume, we finally get:

`\begin{gathered} 4\cdot\mleft(15-5\sqrt[]{(7)/(3)}\mright)^3-180\cdot\mleft(15-5\sqrt[]{(7)/(3)}\mright)^2+2000\cdot\mleft(15-5\sqrt[]{(7)/(3)}\mright) \\ \\ \\ 3000+\frac{7000\sqrt[]{21}}{9}=\text{Maximum volume} \end{gathered}`

This maximum volume is approximately equal to 6564 cubic inches.