Question

A 0.700L sample of gas at STP is compressed to a volume of 0.200L and the temperature is increased to 30 degrees Celcius . What is the new pressure of the gas (in atm)?

Answer 1

Answer: the pressure of the gas after the compression is 3.88 atm

Step-by-step explanation:

The question requires us to calculate the new pressure of a gas, given its initial volume at STP, new volume after compression and temperature after compression.

The following information was provided by the question:

Initial volume = V1 = 0.700 L

Final volume = V2 = 0.200 L

Final temperature = T2 = 30 °C = 303.15 K

To solve this problem, we can apply the equation for ideal gases (shown below) considering the conditions after the compression:

`P* V=n* R* T\rightarrow P_2=(R* n* T_2)/(V_2)`

where R is the constant of gases (R = 0.082057 L.atm/K.mol), n is the number of moles of gas, T2 is the temperature after compression and V2 is the volume after compression.

Note that the number of moles of gas remains the same even after compression. Thus, we can calculate this number of moles considering the inital volume at STP, knowing that 1 mol of a gas at Standard Temperature and Pressure corresponds to 22.4 L of this gas:

22.4 L ------------------------- 1 mol

0.700 L ----------------------- x

Solving for x, we'll have:

`x=((0.700L)*(1mol))/((22.4L))=0.0312mol`

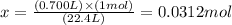
Therefore, the number of moles before and after compression is 0.0312 mol.

Now that we have the values for n, T2 and V2, we can calculate the pressure after compression (P2):

`\begin{gathered} \begin{equation*} P_2=(R* n* T_2)/(V_2) \end{equation*} \\ P_2=((0.082057L.atm/K.mol)*(0.0312mol)*(30+273.15)K)/((0.200L))=3.88atm \end{gathered}`

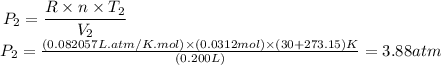
Therefore, the pressure of the gas after the compression is 3.88 atm.