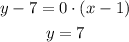Question

Write the equationThe line through (1, 7) and (-6, 7) in point-slope form

Answer 1

`y-7=0\cdot(x-1)`

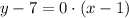
Explanation:

We have that the equation of line in its point-slope form is the following:

`y-y_1=m\cdot(x-x_1)`

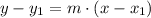
We must calculate the slope, we can do it using the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

We replace the points (1, 7) and (-6, 7) and calculate the value of the slope, like this:

`m=(7-7)/(-6-1)=(0)/(7)=0`

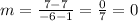
Since the slope is equal to 0, it would not be an equation of a line, since it is a constant, the line through both points would be:

`\begin{gathered} y-7=0\cdot(x-1) \\ y=7 \end{gathered}`