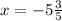Part A
Given the equation
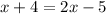
To solve for x, we first collect like terms
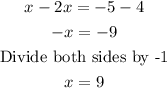
Part B
Given the equation:
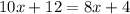
First, we bring all terms containing x to the left-hand side and the constants to the right-hand side.
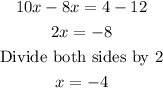
Part C
Given the equation:
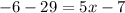
Collect like terms to obtain:
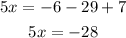
Divide both sides by 5