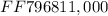We will investigate how to express percentages as decimals ( fractions ). Then we will see how to manipulate these percentages to get the starting or resltant value.
We are asked to determine the " starting number " whose 0.2% would result in the final number:
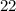
We will first see how to deal with the percentage ( 0.2% ) and the starting number which is an unknown. So lets suppose:

Then we will see how to deal with percentages. The way we deal is by using a basic mathematical operator of ( multiplication ) and convert the percentage into a fraction as follows:
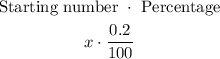
Then we will equate the above expression to the resultant as follows:

Now we have aa full fledged equation. We can easily manipulate and solve for the unknown number ( x ) as follows:
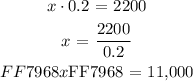
We see the unknown starting number ( x ) is very large as should have been the case. This is due to the fact that ( 0.2% ) is a very small proportion of a number such that it results in a two-digit number like ( 22 ). If the percentage is low but resultant is high, then the starting number must be very large!
Answer: