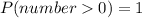Question

See attached photo simple probability

Answer 1

Hello there. To solve this question, we'll have to remember some properties about probabilities.

First, given an event E that can be counted by the number of events Ei that are called favorable events to E happening. Then the probability of E is given by

`P(E)=(n(E_i))/(n(S))`

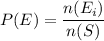
whereas n(S) is the number of events in the sample, also known as the total.

For each case, we'll have to analyze the data and see what is the best approach to solve each of them.

Part A:

As we can see, the spinner contains 7 distinct colors, which means they have the same probability of spinning.

P(purple) is the probability that, among the 7 colors, which means n(S) = 7, we spin purple. The only event favorable to this is when we get purple, hence n(Ei) = 1.

Hence we get

`P(purple)=(1)/(7)`

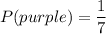
Now we want the probability of spinning Red or Yellow. In this case, we have the probability of an union of events.

Remember that the probability of an union of two events is given by the relation:

`P(A\cup B)=P(A)+P(B)-P(A\cap B)`

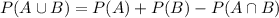
But since the 7 colors are distinct, there are no intersection between the sets for this case, therefore

`P(red\text{ or }yellow)=P(red)+P(yellow)`

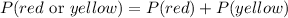
And as for purple, the probability of spinning only red or spinning only yellow is 1/7, hence

`P(red\text{ or }yellow)=(1)/(7)+(1)/(7)=(2)/(7)`

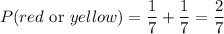
Now, for P(not green), we're looking for the complementary event of getting green. It can be expressed as:

`P(green)+P(not\text{ }green)=P(S)=1`

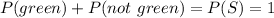
Hence we have

`P(not\text{ }green)=1-P(green)`

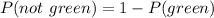
But knowing the probability of getting green is the same as for the other colors, we get

`P(not\text{ }green)=1-(1)/(7)=(7-1)/(7)=(6)/(7)`

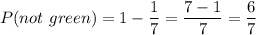
Now, moving to the last question of part A, we want P(not orange or pink)

Notice it doesn't say "nor" pink, hence pink is included here.

Notice also that not orange includes pink, hence we may have an intersection in this case.

For this, we work as follows:

`P(not\text{ }orange\text{ or }pink)=P(not\text{ }orange)+P(pink)-P(not\text{ }orange\text{ and }pink)`

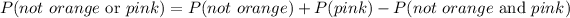
But the case when the color is not orange and pink is the same as the probability when it is pink, hence

`P(not\text{ }orange\text{ and }pink)=P(pink)`

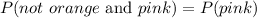
So our probability is simply

`P(not\text{ }orange\text{ or }pink)=P(not\text{ }orange)`

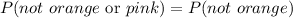
That is the same as when we calculated P(not green), hence

`P(not\text{ o}range\text{ or }p\imaginaryI nk)=(6)/(7)`

=====

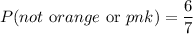
Part B

In this case, we have the six faces of a dice that is rolled and we want to determine

P(3)

This is the probability of getting the face showing 3 up and since there is only an event of getting 3 in the dice, among the six faces, we have n(Ei) = 1 and n(S)=6, hence

`P(3)=(1)/(6)`

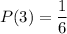
Now, to calculate P(not 4 or 5), we use the same argument we used for P(not orange or pink) on part A;

We'll have

`\begin{gathered} P(not\text{ }4\text{ or }5)=P(not\text{ }4)+P(5)-P(not\text{ }4\text{ and }5) \\ P(not\text{ }4\text{ or }5)=P(not\text{ }4)+P(5)-P(5) \\ \\ P(not\text{ }4\text{ or }5)=P(not\text{ }4)=1-P(4) \\ \\ P(not\text{ }4\text{ or }5)=1-(1)/(6)=(6-1)/(6)=(5)/(6) \\ \\ \end{gathered}`

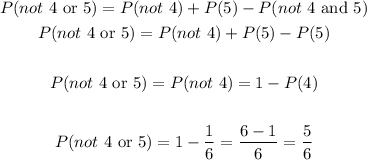
Now, to calculate the probability of getting numbers that are less than 4, we count how many number in the dice faces the numbers are indeed less than 4:

The faces with 1, 2 and 3 dots are the only satisfying this condition, hence n(Ei) = 3 and the probability is given by

`P(number\text{ }<4)=(3)/(6)=(1)/(2)`

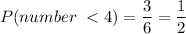
Finally, to get a number that is greater than zero, we don't even need to calculate a probability, since we only have numbers that are greater than zero.

Hence the probability is simply

`P(number>0)=1`