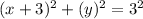Answer:
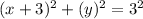
Explanation:
Given the endpoints of the diameter, then the center of the circle is in the middle of the diameter:
The middle point is given as:
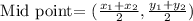
Therefore, the center of the circle is located at:
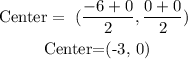
The circle is represented by the following equation:
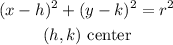
By substituting (h,k) and (x,y) (one of the given points), we can solve for r, to find the radius:
![\begin{gathered} (0-(-3))^2+(0-0)^2=r^2 \\ 9=r^2 \\ r=\sqrt[]{9} \\ r=3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mk6034lrr889hlcu6jsf2yeerejazid62i.png)
Then, this circle is represented by the following equation: