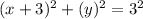Question

Give the equation of a circle with a diameter that has endpoints (-6, 0) and (0,0). Question Help: D Video

Answer 1

`(x+3)^2+(y)^2=3^2`

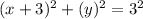
Explanation:

Given the endpoints of the diameter, then the center of the circle is in the middle of the diameter:

The middle point is given as:

`\text{ Mid point= (}(x_1+x_2)/(2),(y_1+y_2)/(2))`

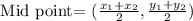
Therefore, the center of the circle is located at:

`\begin{gathered} \text{Center}=\text{ (}(-6+0)/(2),(0+0)/(2)) \\ \text{ Center=(-3, 0)} \end{gathered}`

The circle is represented by the following equation:

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (h,k)\text{ center} \end{gathered}`

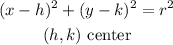
By substituting (h,k) and (x,y) (one of the given points), we can solve for r, to find the radius:

`\begin{gathered} (0-(-3))^2+(0-0)^2=r^2 \\ 9=r^2 \\ r=\sqrt[]{9} \\ r=3 \end{gathered}`

Then, this circle is represented by the following equation:

`(x+3)^2+(y)^2=3^2`