Answer:
F' = 64 N
Explanation:
The force of gravitation between two objects is given by Newton's Law of Gravitation as follows:
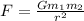 ______________ equation (1)
______________ equation (1)
where,
F = Force = 16 N
G = universal gravitational constant
m₁ = mass of the first object
m₂ = mass of the second object
r = distance between objects
Now, the masses of each object are doubled and the distance between them is same:
m₁' = 2m₁
m₂' = 2m₂
r' = r
Hence, the new force will be:
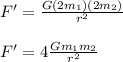
using equation (1), we get:
F' = 4 F = 4(16 N)
F' = 64 N