ANSWER
A) Amplitude: 8
Period: 2π/3
Phase shift: Right π/12
Step-by-step explanation
A sine function can be written in the form,
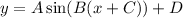
Where A is the amplitude, C is the phase shift left and D is the vertical shift. B is related to the period as follows,
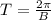
In this case, the given function is,
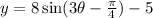
We can see that A = 8, D = -5 and B = 3. Hence, the amplitude is 8 and we have to use the other data to find the phase shift and the period.
If B is 3, then the period is,

To find the phase shift, we have to factor out B,

C is negative, so the phase shift is to the right.
In summary, the amplitude is 8, the period is 2π/3 and the phase shift is π/12 to the right.