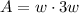Data:
l = 3w
d = 98
To find the area, lets start drawing the field:
The area of rectangle is
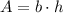
In this case
b = w
h= l = 3w
To determine the value of w, we can use the right triangle and the value of the diagonal that is the hypotenuse of the triangle. Then using Pythagoras theorem:
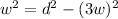
We can clear the w from this equation:
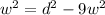
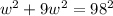
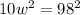
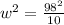
![w=\sqrt[]{(98^2)/(10)}=\sqrt[]{960.4}=30.99\approx40](https://img.qammunity.org/2023/formulas/mathematics/college/xeyab3i8szlvz2h740ffg8wx4c11smudps.png)
Now we know the value of w = 40
Then the area of the field is: