Answer:
C
Explanation:
We are given the function:
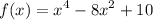
And we want to determine between which consecutive integers are the real zeros of f located.
Because the equation is in quadratic form, we can use the quadratic formula. First, we can let u = x². Then:
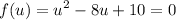
Solve using the quadratic formula:
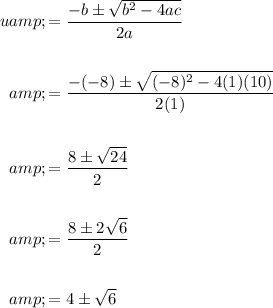
Hence:
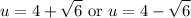
Back-substitute:
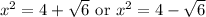
Solve for x:
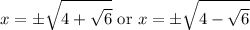
Hence, the four real solutions of x are:
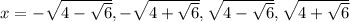
Or, approximately:

Respectively.
Therefore, our answers are both A and B, or simply C.