Question

Scores for a common standardized college aptitude test are normally distributed with a mean of 498 and a standard deviation of 115. Randomly selected men are given a Test Preparation Course before taking this test. Assume, for sake of argument, that the preparation course has no effect.If 1 of the men is randomly selected, find the probability that his score is at least 584.9. P(X > 584.9) = Enter your answer as a number accurate to 4 decimal places.If 7 of the men are randomly selected, find the probability that their mean score is at least 584.9. P(M > 584.9) = Enter your answer as a number accurate to 4 decimal places.

Answer 1

Consider X to be the random variable representing the score of any man.

The mean and standard deviation are given to be 498 and 115 respectively,

`\begin{gathered} \mu=498 \\ \sigma=115 \end{gathered}`

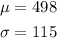
The standard normal variate corresponding to any value of score, is given by the formula,

`z=(x-\mu)/(\sigma)`

For X=584.9, the z-score becomes,

`\begin{gathered} z=(584.9-498)/(115) \\ z=(86.9)/(115) \\ z=0.75 \end{gathered}`

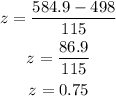
Then the probability that a randomly selected man has scored at least 584.9 is calculated as,

`P(X\ge584.9)=P(z\ge0.75)`

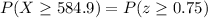
Using the properties of normal distribution,

`\begin{gathered} P(X\ge584.9)=P(z\ge0)-P(0\leq z\leq0.75) \\ P(X\ge584.9)=0.5-\varnothing(0.75) \end{gathered}`

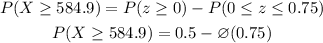
From the Standard Normal Distribution Table,

`\varnothing(0.75)=0.2734`

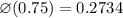
Substitute the value,

`\begin{gathered} P(X\ge584.9)=0.5-0.2734 \\ P(X\ge584.9)=0.2266 \end{gathered}`

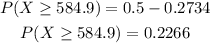
Thus, there is a 0.2266 probability that the score of a randomly selected man is at least 584.9.

Consider a normal sample of 7 men from the college,

`n=7`

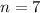
The z-score for the random sample is given by,

`z=\frac{x-\mu}{\frac{\sigma}{\sqrt[]{n}}}`

Substitute the values,

`\begin{gathered} z=\frac{584.9-498}{\frac{115}{\sqrt[]{7}}} \\ z=\frac{86.9\sqrt[]{7}}{115} \\ z=2.00 \end{gathered}`

So the probability that the mean of the sample is at least 584.9, is calculated as,

`P(X_s\ge584.9)=P(z\ge2)`

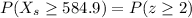
Using the properties of Normal Distribution,

Substitute the value,

`\begin{gathered} P(X_s\ge584.9)=0.5-0.4772 \\ P(X_s\ge584.9)=0.0228 \end{gathered}`

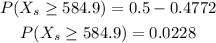
Thus, there is a 0.0228 probability that their mean score is at least 584..9.