Given:
![a_n\text{ represents the number of autism cases diagnosed in the United States, in thousands , n years after 2000.}]()
a)
We get the following values from the graph.
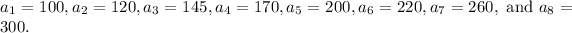
b)
The given nth term of the sequence is
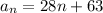
Required:
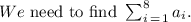
Step-by-step explanation:
a)
Expand the sum.
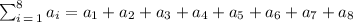
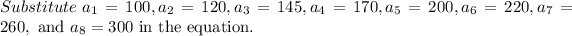
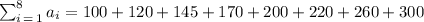
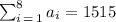
b)
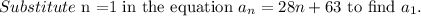
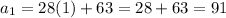
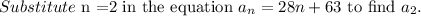
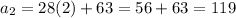
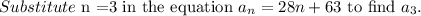
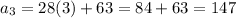
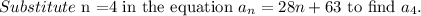
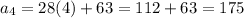
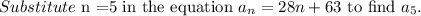
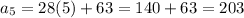
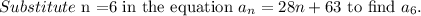
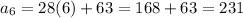
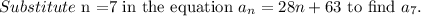
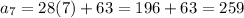
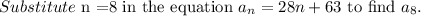
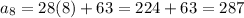
Consider the summation.
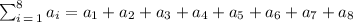
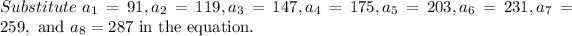
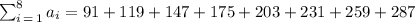
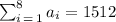
The actual sum is 1515 which is greater than 1512
So this value is underestimated.
Final answer:
a)
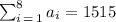
b)
Underestimated.