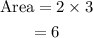Question

Find the area of a parallelogram bounded by the y-axis, the line x=3, the line f(x)=1+2x, and the line parallel to f(x) passing through (2,7).The area is Answer square units

Answer 1

Given:

`\begin{gathered} f(x)=2x+1 \\ x=3 \end{gathered}`

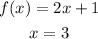
Parallel line slope are also same then parallel line equation is:

`f(x)=2x+k`

The line pass (2,7) then:

`\begin{gathered} f(x)=2x+k \\ 7=2(2)+k \\ 7=4+k \\ k=7-4 \\ k=3 \end{gathered}`

So two parallel line equation is :

`\begin{gathered} f(x)=2x+1 \\ f(x)=2x+3 \end{gathered}`

As the difference in y intrcepts is 2.

The side of parallelogram along y- axis is 2.

Two other parallel line are x=0 and x=3

so vertical distance between them is 3

so area is:

`\begin{gathered} \text{Area}=2*3 \\ =6 \end{gathered}`