Question

A figure has a perimeter of 40 units and an area of 100 units. Which of the following describes the new perimeter and area after the figure is dilated by ascale factor of 1/2PLEASE HELPPPP-

Answer 1

We will investigate how the dilation factor effects the perimeter and the area of an arbitrary figure.

A dilation factor is used to scale up or down an actual figure. The scaling of any figure involves the enlargement or shrinking of each and every side of an arbitrary figure by the factor defined.

We are given an arbitrary figure which has the following details pertaining to the perimeter ( P ) and area ( A ):

`\begin{gathered} P_i\text{ = 40 } \\ A_i\text{ = 100} \end{gathered}`

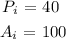
We are given that the above figure undergoes a dilation transformation with a scale factor ( F ) of:

`\text{Scale Factor = }(1)/(2)`

To consider the effect of scale factor on the original perimeter ( P ) and area ( A ) we will resort to the basic definitions of each.

A perimeter is the sum of all sides of an figure and expressed as follows:

`P\text{ = }\sum ^N_(i\mathop=1)(x_i)`

Whereas, an area is the multiplication of induvidual sides of a figure:

`A=x_1\cdot x_2\cdot\ldots`

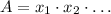
When we apply the dilation factor we need to keep in mind that it affects the length of each side of a figure and scale up or down the original length. So for the given scale factor we can write:

`\begin{gathered} P\text{ = }\sum ^N_(i\mathop=1)(F\cdot x_i) \\ \\ P\text{ = F}\cdot\sum ^N_(i\mathop=1)(x_i) \end{gathered}`

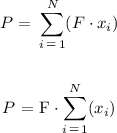
And,

`\begin{gathered} A\text{ = (F}\cdot x_1)\cdot(F\cdot x_2)\text{ } \\ A=F^2\cdot(x_1\cdot x_2) \end{gathered}`

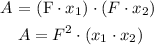
Plugging in the scale factor in above two general definitions we have the following parameters of Area ( A ) and Perimeter ( P ) for the dilated figure:

`\begin{gathered} P\text{ = }(1)/(2)\cdot P_i \\ A\text{ = }(1)/(4)\cdot A_i \end{gathered}`

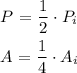
Therefore, the Perimeter is halved and the area is cut off a quarter. The parameters of the image of the transformation turn out to be:

`\begin{gathered} P\text{ = }(40)/(2) \\ P\text{ = 20 units} \\ \\ A\text{ = }(1)/(4)\cdot100 \\ A=25units^2 \end{gathered}`

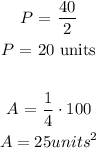
Hence, the option B is correct!