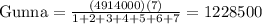We are given that a quantity of $4914000 is divided in the ratio of 1:2:3:4:5:6:7. To determine the amount for each one, let's remember that when a quantity "N" is divided in the ratio of x:y:z:d..., then each part corresponds to:
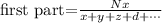
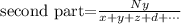
And so on. Therefore, the part of Roddy Rich is:
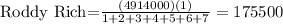
the part of lil babe is
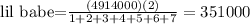
Jay cole part is:
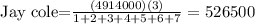
Da baby part:
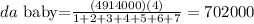
Young thug part:
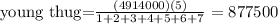
Future part:
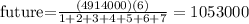
Gunna part: