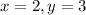The two equations given are:
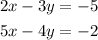
The coefficient matrix A is:
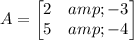
The variable matrix X is:
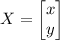
and the constant matrix B is:
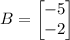
Then, AX = B looks like,
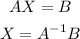
So, the variables "x" and "y" are found my multiplying the inverse of A by the matrix B.
Let's find the inverse matrix of A:
Given, a 2 x 2 matrix,
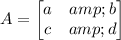
The inverse of this matrix will be,
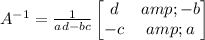
Using the formula, we have:
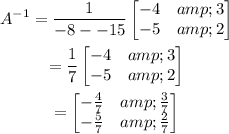
Now, we can solve for the matrix X, shown below:
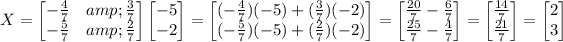
The solution matrix, X, is
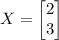
This, means the solution to the system of equations is: