Step 1
Given; The General Social Survey included a question about how many hours the respondent spent doing volunteer activities outside of their own home. For the 515 respondents, the sample mean was 6.15 hours and the sample standard deviation was 16.53 hours. Find the value of the multiplier needed to compute a 95% confidence interval for the population mean amount of time spent doing volunteer activities outside of their own home.
Step 2
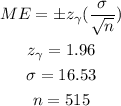

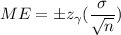
Answer;
