If the missing side is 12in the sides must satisfy the Pythagorean theorem

For the first option, we have 8in,12in,17 in
where
a=8in
b=12in
c=17 in
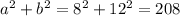
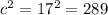
the results are different therefore it is not a right triangle with a missing side of 12.
For the second option, we have 12in, 20in,25in
a=12 in
b=20 in
c=25 in

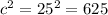
the results are different therefore it is not a right triangle with a missing side of 12.
For the third option, we have 5in, 12in, 13in
a=5 in
b=12 in
c=13 in
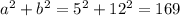
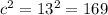
It is a right triangle with a missing side of 12 in
For the fourth option, we have 9in, 12 in 15 in
a=9in
b=12in
c=15 in
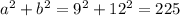
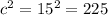
It is a right triangle with a missing side of 12 in
For the fifth option, we have 12in ,60in, 61in
a=12in
b=60in
c=61in

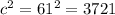
the results are different therefore it is not a right triangle with a missing side of 12.
For the sixth option we have 12 in, 35 in, 37 in
a=12in
b=35 in
c=37 in

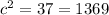
It is a right triangle with a missing side of 12 in