Answer: FALSE
Step-by-step explanation:
The rule to determine if three sides can form a triangle is that the sum of any two sides must be greater than the third side.
Let a, b, and c be the sides of the triangle:
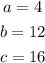
The rule is that the following three inequalities must be met:
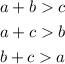
Calculating these inequalities to check if they are all true or not:
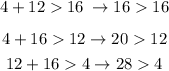
The first inequality is not true, because 16 is not greater than 16 (it is equal to 16 but not greater than 16). The other two inequalities are true: 20 is greater than 12 and 28 is greater than 4.
Since one of the inequalities is not true, the lengths can not form a triangle.
Answer: FALSE