Explanation:
Step 1. We need to find the option for which the domain is:
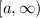
and the range
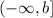
Step 2. Let's start with the domain. The domain is the set of possible x values.
when we have a square root, the value inside the square root has to be greater than or equal to 0, for options B and D:
Solving for x on each inequality:
Step 3. That means that for B, the domain is:
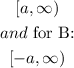
Only B meets the condition for the domain, since the other two options A, and C has third roots, the values inside of them can be negative and the domain is not [a, infinity).
Step 4. If we graph the function for option B, here we are using a=1 and b=2 but these could be any values since it is just for demonstration
We can see that the values possible for the y-axis (the range) go from minus infinity and stop at value b.
Therefore, option B also has the correct range.
Answer.
B
