Question

Two cyclists are on a straight road, with cyclist B initially 30 metes ahead of cyclistA.Cyclist A maintains a constant velocity of 21 m s^-1, whilst cyclist B is initially at restbut accelerates uniformly at 6 m s^-2Find the two times when the cyclists are level with each other.

Answer 1

We are given that a cyclist A is moving at a constant speed of 21 m/s. The equation of position with respect to the time of an object moving at a constant speed is the following:

`x=x_0+vt`

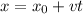
Where:

`\begin{gathered} x=\text{ position} \\ x_0=\text{ initial position} \\ v=\text{ velocity} \\ t=\text{ time} \end{gathered}`

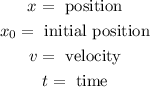
Substituting the values we get:

`x=21t`

Cyclist B starts at the position 30 meters is moving at a constant acceleration. The formula for the position of an object moving at a constant acceleration is the following:

`x=x_0+v_0t+(1)/(2)at^2`

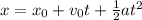
Where:

`\begin{gathered} v_0=\text{ initial velocity} \\ a=\text{ acceleration} \end{gathered}`

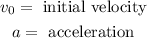
Since the object begins at rest this means that the initial velocity is zero. If we set its starting point at the origin then the initial position is zero. Now, we substitute the values:

`x=30+(1)/(2)(6(m)/(s^2))t^2`

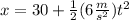
Solving the operations:

`x=30+3t^2`

Since we are asked to determine the time when they are at the same distance we need to set both equations equal:

`21t=30+3t^2`

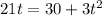
Now, we divide both sides by 2;

`7t=10+t^2`

Now, we subtract "7t" from both sides:

`t^2-7t+10=0`

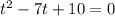
We get an equation of the form:

`at^2+bt+c=0`

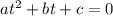
To solve the equation we will factor the left side:

`(t+*)(t+*)=0`

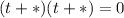
We need to find two numbers such that their product is 10 and their algebraic sum is -7. Those numbers are -5 and -2:

`(t-5)(t-2)=0`

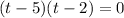
Now, we set both factors equal:

`\begin{gathered} t-5=0 \\ t=5 \end{gathered}`

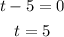
For the second factor:

`\begin{gathered} t-2=0 \\ t=2 \end{gathered}`

The two times are then 5s and 2s.