Question

The Gulf stream is a warm ocean current that extends from the Eastern side of the Gulf of Mexico up through the Florida straits and along the Southeastern Coast of the United States to Cape Hatteras, North carolina. a boat travels with the current 110 miles from Miami, florida, to freeport, Bahamas in 5 hours. the return trip against the same current takes 9 and 1/6 hour. find the speed of the boat and still water and the speed of the current.

Answer 1

Speed of current: 5 miles per hour

Speed of the boat in still water: 17 miles per hour

Step-by-step explanation:

Let us call sB the speed of the boat in still water and sC the speed of the current.

Now when the boat is with the current, its speed is 110 miles/hours = 22 miles per hour. When the boat is opposite the current, its speed is 110 / (9 + 1/6 ) = 12 miles per hour; therefore we have the equations

`s_b+s_c=22\text{ (with the current )}`

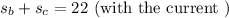
and

`s_b-s_c=12\text{ (opposite the current)}`

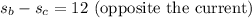
adding the two equations gives

`\begin{gathered} s_b+s_c=22 \\ s_b-s_c=12 \\ ---------------- \\ 2s_b=34 \end{gathered}`

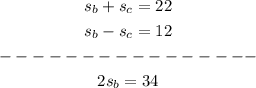
dividing both sides by 2 gives

`\begin{gathered} s_b=(34)/(2) \\ s_b=17 \end{gathered}`

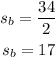
Hence, we find that the speed of the boat in still water is 17 miles per hour.

Now with the value of sB in hand, we now find sC.

`\begin{gathered} s_b+s_c=22 \\ 17+s_c=22 \end{gathered}`

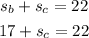
subtracting 17 from both sides gives

`s_c=5`

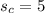
Hence, the speed of the current is 5 miles per hour.

To conclude,

Speed of current: 5 miles per hour

Speed of the boat in still water: 17 miles per hour