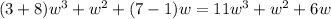Question

Identify and combine the liked terms3w³ + 7w + 8w³ + w²-w =

Answer 1

To solve this problem, first we should identify the shape of the expression. Every term is an expression of the same letter (w), which in this case is our variable. Now, we should identify liked terms. To do so, recall that our terms are of the form

`aw^n`

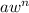
so, to identify liked terms, they should have the same value of n. For example, in this case, note that the terms

`3w^3,8w^3`

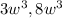
they have the same value of n (in this case 3).

So, using this, we can identify the rest of the same terms are put them together, so we get

`3w^3+8w^3+w^2+7w\text{ -w}`

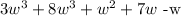
Now, the coefficients of the liked terms can operated with each other as follows:

`3w^3+8w^3+w^2+7w-w=(3+8)w^3+w^2+(7\text{ -1)w}`

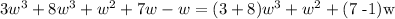
which is the expression

`(3+8)w^3+w^2+(7-1)w=11w^3+w^2+6^{}w`