To determine if the given lines are perpendicular, parallel, intersecting, or identical, the first step is to write both equations in slope-intercept form:
First equation:
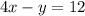
To write the equation in slope-intercept form, the objective is to leave the y-term alone on the left side of the equation and all other terms on the right side of it.
The first step is to pass "4x" to the right side of the equal sign, to do so you have to apply the opposite operation "-4x" to both sides of the equal sign:
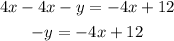
Next, the y-term is negative, but we need it to be positive. To change the sign of the term, you have to multiply it by "-1", and, to keep the equality valid, any operation done to one side of the equal sign must be done to the other side as well. So you have to multiply both sides by "-1":
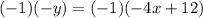
Finally, solve the multiplication on the left side of the equation and distribute and solve the multiplication on the right side:
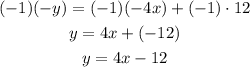
The first equation written in slope-intercept form is:
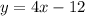
Second equation:
The second equation is already given in the slope-intercept form:
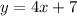
Now, when you compare the equations of two lines, the most important term to compare is the slope of the lines:
If their slopes are equal, then the lines are parallel.
If their slopes are reverse opposites, then the lines are perpendicular.
If their slopes are different, then the lines might intercept at one point.
If both equations are the same or lead to the same equation when simplified, then both lines are identical.
The slope of the first equation is m=4 and the slope of the second equation is m=4. Both equations have the same slope which means they are parallel lines.