Answer:
45 feet
Step-by-step explanation:
We are required to find the height of the kite above the ground.
• The side opposite angle 55 degrees = x
,
• The length of the hypotenuse = 50 ft
From trigonometric ratios:

Therefore:
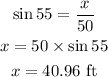
Since the distance from the ground to Penny's hand is 4 feet, the height of the kite above the ground will be:
