Step 1:
Let y represent the cost C and let x represent the number of lessons.
Step 2:
Write the formula for two points forms of the equation of a linear equation.
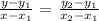
Step 3:
Write the given data
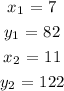
Step 4:
Substitute the values in the formula
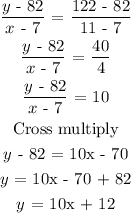
Step 5:
Write the equation
C = 10L + 12
Part 2
The cost for 4 lessons
L = 4, C = ?
From the equation C = 10L + 12
C = 10 x 4 + 12
C = 40 + 12
C = $52