Solution:
Given the table as shown below:
Using the equation:

When x = 68, y equals 4.1.
Thus, substitute these values into equation 1
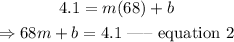
When x = 71, y equals 4.6.
Similarly, we have
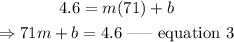
From equation 2, make c the subject of the formula.
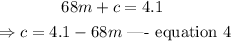
Substitute equation 4 into equation 3. Thus,
![\begin{gathered} 71m+c=4.6\text{ } \\ \Rightarrow71m+(4.1-68m)=4.6 \\ \text{open parentheses} \\ 71m+4.1-68m=4.6 \\ \text{collect lik terms} \\ 71m-68m=4.6-4.1 \\ 3m=0.5 \\ \text{divide both sides by the coefficient of m, which is 3.} \\ \text{thus,} \\ m=(0.5)/(3) \\ \Rightarrow m=(1)/(6) \end{gathered}]()
Substitute the obtained value of m into equation 4.
thus,
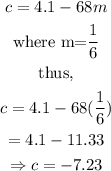
Hence, (x,y) Notation y=mx+c
![undefined]()