Answer:
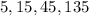
Step-by-step explanation:
Given the nth term of the required sequence expressed according to the equation:
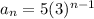
You need to get the first four terms of the sequence as shown:
For the first term, when n = 1
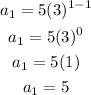
For the second term, when n = 2
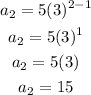
For the third term, when n = 3
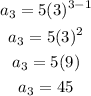
For the fourth term, when n = 4
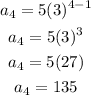
Therefore the first four terms of the sequence will be 5, 15, 45 and 135