a) The fiven function is
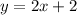
This equation represents a linear function, it indicates that for each increase of x, y increases 2 units.
To graph this function you have to determine two points of the line, plot them and cross them with a line.
Since the equation is in slope, intercept form, we can tell directly from it that the y-intercept is (0,2)
For the second point use any value of x and replace it in the formula, for example x=1
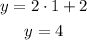
For x=1 correspond y=4, that is the second point (1,4)
Next plot the line
b) For the equation

This equation corresponds to a parabola, i.e. a quadratic function. This is determined because x is squared, this means that, for example for x=-2 and x=2 the function will have the same value of y, except at its vertex.
To draw this function you have to determine its vertex and